Mathmatical expression

For scientific purpose, we sometime need to shift phase of time series with specfic angles. To acheive this, we can transform the time series into freqeuency domain with $$F(\omega) = \int_{-\omega}^{\omega} f(t) e^{-i \omega t} dt$$

where $F(\omega)$ as Fourier spectrum of signal $f(t)$. Thus, the phase shifted Fourier spectrum $F_{sh}$ is

$$F_{sh}(\omega) = F(\omega) * e^{-i \alpha}$$

in thich $\alpha$ indicates shifted angle.

Numerical experiment

Previous approach could be applied with below Python code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73

# -*- coding: utf-8 -*-
#-------------------------------------------------------------------------------
#      Purpose: Shown edge error in performing phase shift
#       Status: Developing
#   Dependence: Python 3.6
#      Version: ALPHA
# Created Date: 22:11h, 29/07/2018
#        Usage: python test.py
#       Author: Xiao Xiao, https://github.com/SeisPider
#        Email: xiaox.seis@gmail.com
#     Copyright (C) 2017-2018 Xiao Xiao
#-------------------------------------------------------------------------------
from numpy.fft import rfft, irfft, rfftfreq
from scipy.signal import hilbert
import numpy as np
import matplotlib.pyplot as plt
import matplotlib
font = {'size'   :  18}
matplotlib.rc('font', **font)

def phase_shift(iptsignal, angle, dt):
    """Perform phase shift of arbitary angle

    Parameter
    =========
    iptsignal : numpy.array
        input signal
    angle : float
        angle to shift signal, in degree
    dt : float
        time step
    
    """
    # Resolve the signal's fourier spectrum
    spec = rfft(iptsignal)
    freq = rfftfreq(iptsignal.size, d=dt)

    # Perform phase shift in freqeuency domain
    spec *= np.exp(1.0j * np.deg2rad(angle))

    # Inverse FFT back to time domain
    phaseshift = irfft(spec, n=len(iptsignal))
    return phaseshift

if __name__ == '__main__':
    # Define Time range
    time = np.arange(0, 10000)
    signal = np.cos(time /  100.0)
    sinsignal = np.sin(time /  100.0)
    
    # Shift angle and time step
    angle, dt = -90, 1
    phsignal = phase_shift(signal, angle, dt)

    # Comparasion between Personal shifted and theoretical result
    fig, axes = plt.subplots(nrows=2, ncols=1, figsize=(12, 14))
    axes[0].plot(time, signal, label="Cosine (raw)")
    axes[0].plot(time, sinsignal, label="Sine")
    axes[0].plot(time, phsignal, "--", label="Shift")
    axes[0].set_xlabel("Time")
    axes[0].set_ylabel("Amplitude")
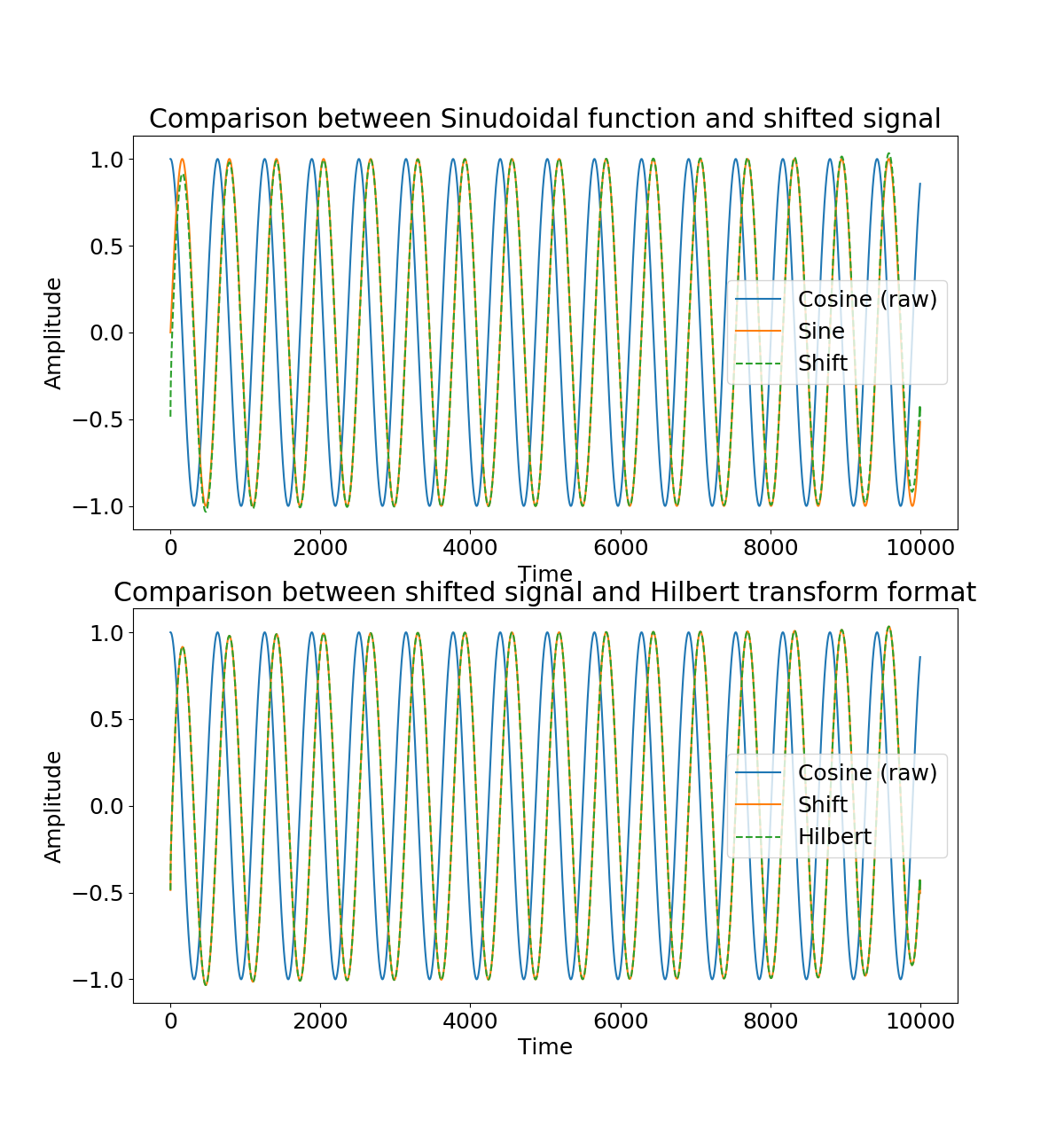
    axes[0].set_title("Comparison between Sinudoidal function and shifted signal")
    axes[0].legend()

    # Comparasion between Personal shifted and Hilbert transform result
    axes[1].plot(time, signal, label="Cosine (raw)")
    axes[1].plot(time, phsignal, label="Shift")
    axes[1].plot(time, np.imag(hilbert(signal)), "--", label="Hilbert")
    axes[1].set_xlabel("Time")
    axes[1].set_ylabel("Amplitude")
    axes[1].set_title("Comparison between shifted signal and Hilbert transform format")
    axes[1].legend()
    plt.show()

With an output like below,

Output of previous code

Using a cosine-dominated signal for benchmark, the theoretical phase shifted signal shold be a sine signal with same frequency. However, the phase shifted signal shows great differences in edge part refering to the theoretical one and is the same as the signal computed from numerical hilbert tranformation result.

warning

So, it’s dangerous to numerically shift phases and completely wrong in edge part, around 2~3 times of the maximum peroid.

Change log.

  • 2018-07-29: Initial version